2.6 Lexicographical Numbers

Description

Given an integer n, return 1 - n in lexicographical order.

For example, given 13, return: [1,10,11,12,13,2,3,4,5,6,7,8,9].

Please optimize your algorithm to use less time and space. The input size may be as large as 5,000,000.

Method

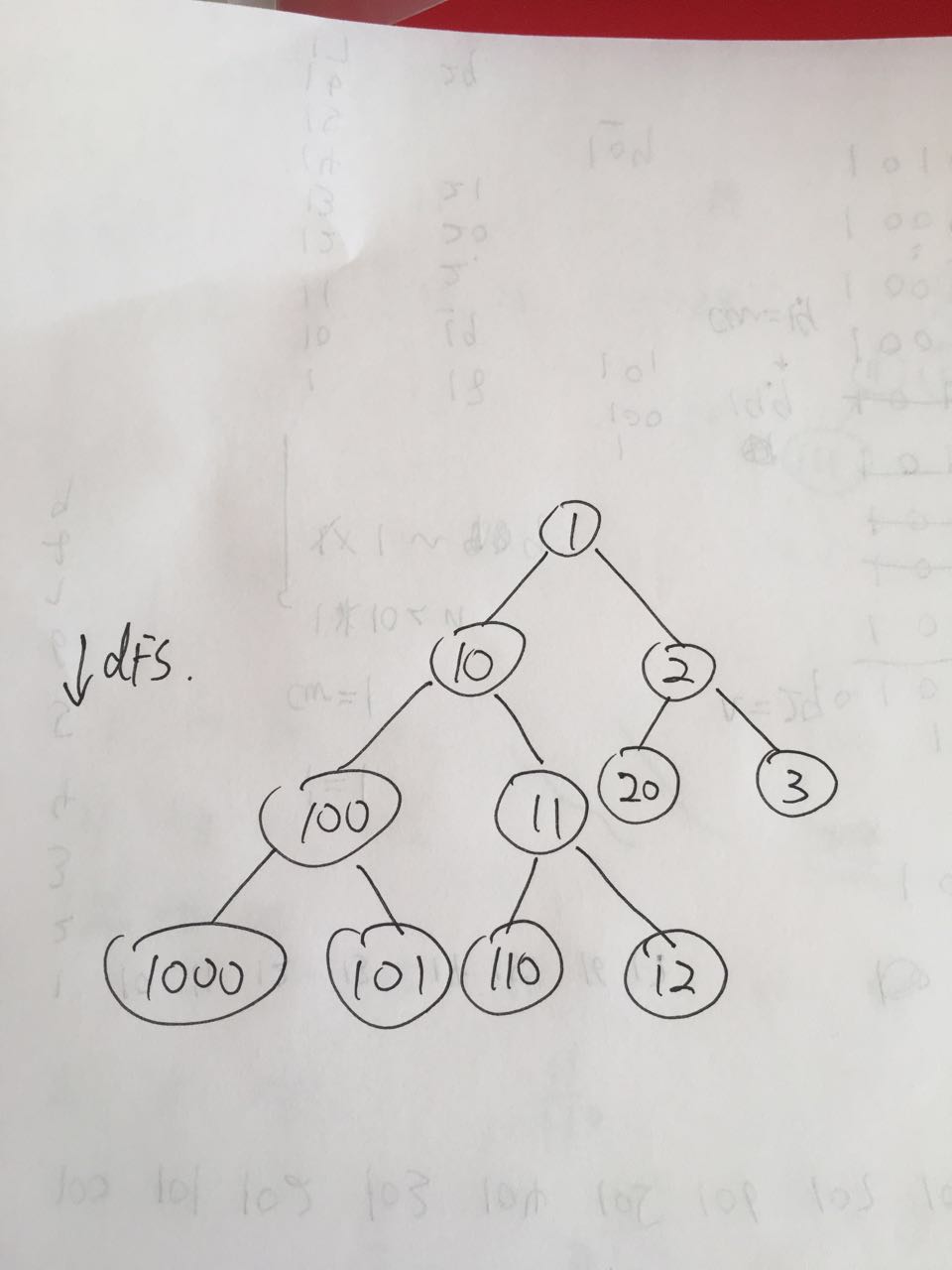
The basic idea is to find the next number to add. Take 45 for example: if the current number is 45, the next one will be 450 (450 == 45 * 10)(if 450 <= n), or 46 (46 == 45 + 1) (if 46 <= n) or 5 (5 == 45 / 10 + 1)(5 is less than 45 so it is for sure less than n). We should also consider n = 600, and the current number = 499, the next number is 5 because there are all "9"s after "4" in "499" so we should divide 499 by 10 until the last digit is not "9".

it use tree structure and dfs.

Time and Space Complexity

O(n) times and O(1) extra space

Code

public class Solution {

public List<Integer> lexicalOrder(int n) {
       List<Integer> res = new ArrayList<Integer>();
       int cur = 1;
       for (int i = 1; i <= n; i++){
            res.add(cur);
            if (cur * 10 <= n){
                cur = cur * 10;
            } else {
               // to return to the root parent from left subtree
                while ( cur % 10 == 9 || cur == n){
                    cur /= 10;
                }
                // go to right subtree
                cur++;
            }
       }
       return res;
}

}